前言随着天气越来越冷，我们的身体消耗也越来越大，这个时候，我们需要持续的营养输入来保持强健的体态，而牛肉是最为简单直接、且优质的营养来源，牛肉富含氨基酸、磷脂、维生素B6、维生素B12、烟酸、钙、铁、锌、锰等营养物质，有助于恢复体力、补益气血、促进代谢、强壮筋骨、提升抵抗力，因此，冬季炖牛肉是一个非常好的进补方式，炖牛肉的技巧想要炖出...。

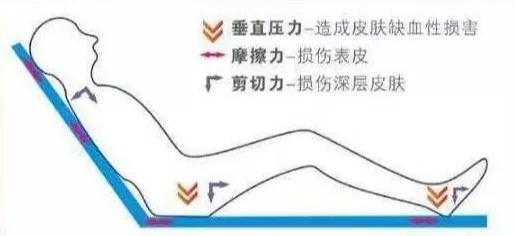
住院老年患者，即使是可以自行行走者，大多数时间都在床上度过，而这会导致院后综合征，即出院后会处于一段脆弱期，这与一般的身体状况下降有关，研究者表示，如果不积极管理，可能会增加再入院、残疾、需要护理、疾病或死亡风险，研究显示，抵消卧床休息不良影响并改善老年住院患者机体机能所需要的最小运动剂量，估计为每日约40分钟的轻度体力活动，或每日约...。

纳维尔，斯托克斯方程是流体力学中描述流体运动的重要方程，它与牛顿运动定律有着密切的联系，牛顿运动定律描述作用在物体上的合力等于物体的质量与加速度的乘积，而纳维尔，斯托克斯方程描述作用在流体微元上的合力等于流体微元的质量与其加速度的乘积，以及来自流体粘度的力，矢量计算的张量化在传统的流体力学中，矢量微积分被用来进行矢量计算，使用张量语言...。

发表在，英国运动医学杂志，的一项研究对现有证据进行的汇总数据分析表明，每日只需慢走25分钟，似乎就足以抵消卧床休息对老年患者的不良影响，住院老年患者，即使是可以自行行走者，大多数时间都在床上度过，而这会导致院后综合征，即出院后会处于一段脆弱期，这与一般的身体状况下降有关，研究者表示，如果不积极管理，可能会增加再入院、残疾、需要护理、疾...。

发表在，英国运动医学杂志，的一项研究对现有证据进行的汇总数据分析表明，每日只需慢走25分钟，似乎就足以抵消卧床休息对老年患者的不良影响，卧床休息对老年患者的影响住院老年患者，即使是可以自行行走者，大多数时间都在床上度过，而这会导致院后综合症，即出院后会处于一段脆弱期，这与一般的身体状况下降有关，研究者表示，如果不积极管理，可能会增加再...。

理解纳维尔，斯托克斯方程导言纳维尔，斯托克斯方程是流体力学中的一组基本方程，描述了流体的运动，这些方程源自牛顿运动定律，但表述方式不同，更适合流体动力学的分析，本文将从张量语言的角度介绍如何理解纳维尔，斯托克斯方程，并探讨其与牛顿运动定律之间的关系，张量语言在流体力学中的应用传统的流体力学教科书中，矢量微积分被用作数学工具，张量语言在...。

根据发表在，英国运动医学杂志，的一项研究，每天只需慢走25分钟，似乎就足以抵消卧床休息对老年患者的不良影响，住院老年患者，即使是可以自行行走者，大多数时间都在床上度过，而这会导致院后综合征，即出院后会处于一段脆弱期，这与一般的身体状况下降有关，研究者表示，如果不积极管理，可能会增加再入院、残疾、需要护理、疾病或死亡风险，这项研究分析了...。

纳维尔，斯托克斯方程是一组偏微分方程，描述了粘性流体的运动，它们以物理学家克劳德，路易·纳维尔和乔治·加布里埃尔·斯托克斯的名字命名，他们在19世纪独立推导出这些方程，纳维尔，斯托克斯方程可以用来描述从血液流动到湍流的各种流体现象，它们在许多工程和科学领域都至关重要，包括航空航天、海洋工程和生物流体力学，纳维尔，斯托克斯方程与牛顿运动...。

最近发表在，英国运动医学杂志，上的一项研究对现有证据进行的汇总数据分析表明，每日只需慢走25分钟，似乎就足以抵消卧床休息对老年患者的不良影响，卧床休息对老年患者的影响住院老年患者，即使是可以自行行走者，大多数时间都在床上度过，而这会导致院后综合征，即出院后会处于一段脆弱期，这与一般的身体状况下降有关，研究者表示，如果不积极管理，可能会...。

纳维尔，斯托克斯方程的理解纳维尔，斯托克斯方程是流体力学的基本方程，描述了流体运动的运动学和动力学，这个方程以其复杂性和求解困难而闻名，但也因为它能准确描述各种流体现象，如湍流、空气动力学和地球物理学，而备受推崇，纳维尔，斯托克斯方程可以通过张量分析来简化和理解，这是一种将矢量和张量用于数学和物理计算的框架，张量分析在流体力学中的应用...。

前言在流体力学领域，纳维尔，斯托克斯方程是一组重要的偏微分方程，描述了流体的运动和行为，本篇文章将探讨如何理解纳维尔，斯托克斯方程，它与牛顿运动定律的关系，以及如何利用张量语言简化流体力学中的矢量计算，张量语言的优势在传统的矢量微积分中，流体力学中的计算往往复杂且繁琐，利用张量语言，我们可以显著简化这些计算，张量是描述物理量的多维数组...。

纳维尔，斯托克斯方程是流体力学中描述流体运动的基本方程，它描述了流体的速度、压力和温度随时间和空间的变化，该方程非常复杂，因此使用张量分析对其进行简化非常重要，牛顿运动定律与纳维尔，斯托克斯方程牛顿运动定律用于描述物体的运动，根据第三定律，作用在物体上的合力等于其质量与加速度的乘积，对于流体微元，作用在微元上的合力包括压力梯度和粘滞力...。

纳维尔，斯托克斯方程是流体力学中的一个基本方程，它描述了流体的运动，它是一个偏微分方程，通常简写为，```ρ，∂v，∂t，ρ，v⋅∇，v=，∇p，μ∇²v```其中，ρ是流体的密度v是流体速度p是流体的压力μ是流体的粘度```这个方程可以从牛顿第三定律推导出来，即作用力等于反作用力，考虑流体微元受到的力，根据牛顿第三定律，该力等于流...。

肺肿瘤患者出现肩膀疼痛可能是由于多种原因引起的，肺癌可能会转移至骨骼系统，导致骨质破坏，从而引起肩膀疼痛，肺癌晚期可能会出现肺部感染，导致肩周炎，进而引起肩膀疼痛，肺癌患者的身体较为虚弱，如果长期从事重体力劳动，可能会导致肌肉劳损，从而引起肩膀疼痛，肺肿瘤患者肩膀疼痛的原因肺部肿块压迫，当肺部肿瘤逐渐增大时，可能会对周围组织产生压迫作...。

1️⃣水瓶座，1.20，2.18，主题，浪漫升温今天的恋爱运极佳，和伴侣的关系如鱼得水，甜蜜氛围随处可见，在这个周末放下繁忙日常，享受彼此时光的好日子吧，幸运物品，香水瓶幸运金句，爱是奇妙的魔法，愿它点亮你的每一天，2️⃣双鱼座，2.19，3.20，主题，能量满满今天你会发现自己的体力和精神状态都不错，特别适合面对工作中的挑战和机会，...。

水瓶座，1.20，2.18，主题，浪漫升温今天的你恋爱运极佳，和伴侣的关系如鱼得水，甜蜜氛围随处可见，在这个周末放下繁忙日常，享受彼此时光的好日子吧，幸运物品，香水瓶幸运金句，爱是奇妙的魔法，愿它点亮你的每一天，双鱼座，2.19，3.20，主题，能量满满今天你会发现自己的体力和精神状态都不错，特别适合面对工作中的挑战和机会，维持现有的...。

引言了解纳维尔，斯托克斯方程对于理解流体力学至关重要，而张量语言可以大大简化流体力学中的矢量计算，本文将探讨纳维尔，斯托克斯方程、牛顿运动定律和张量语言之间的关系，纳维尔，斯托克斯方程纳维尔，斯托克斯方程描述了流体的运动，是流体力学中的基本方程之一，该方程可以解释流体的粘性、密度和速度之间的关系，它等式右边的压强梯度项和粘滞项，恰好对...。

引言纳维尔，斯托克斯方程是流体力学中描述流体运动的基本方程组，它以牛顿第三定律为基础，表达了流体微元所受力的平衡关系，本文将从张量语言的角度出发，介绍如何理解纳维尔，斯托克斯方程，以及它与牛顿运动定律之间的关联，张量语言在流体力学中的应用张量语言是一种用于描述多维空间中矢量和二阶张量及其运算的数学工具，在流体力学中，张量语言可以极大地...。

纳维尔，斯托克斯方程是流体力学中的基本方程之一，它描述了流体的运动，方程的复杂性使得直接理解它变得困难，通过张量语言，我们可以简化流体力学中的矢量计算，从而更好地理解纳维尔，斯托克斯方程，张量语言简化流体力学矢量计算张量是一种数学对象，它可以表示具有多个分量的物理量，在流体力学中，我们可以使用张量来描述流体的应力和粘度，通过使用张量语...。

纳维尔，斯托克斯方程是流体力学中的基本方程，描述了流体的运动，它是一个偏微分方程组，包含速度、压力和温度等流场变量，与牛顿运动定律的关系纳维尔，斯托克斯方程可以从牛顿第三定律推导而来，牛顿第三定律指出，作用在物体上的力等于物体对力的反作用力，对于流体微元，其受到的力包括压力梯度和粘滞力，张量语言在流体力学中的应用张量语言是一种数学工具...。

导言纳维尔，斯托克斯方程是流体力学中的基本方程，描述了流体的运动，它们以法国工程师克劳德，路易·纳维和英国数学家乔治·加布里埃尔·斯托克斯命名，与牛顿运动定律的关系纳维尔，斯托克斯方程是牛顿第三定律在流体中的表达，牛顿第三定律指出，作用在物体上的每一个作用力都对应着一个大小相等、方向相反的反作用力，在流体中，作用在流体微元上的作用力包...。

唐欣，江苏女排的超级新星提到唐欣，就不得不先聊聊她在江苏女排与天津女排的那场关键对决中令人惊叹的表现，在这场备受瞩目的较量中，唐欣不仅全场被对手追发，却表现异常稳定，即便是打到第五局，体力也没有明显下滑，更难能可贵的是，她在进攻端展现出极高的效率和稳定性，暴力扣球频频得分，成为江苏女排战胜天津女排的重要功臣，这位年仅20岁的年轻主攻，...。

前言纳维尔，斯托克斯方程是流体力学的基础方程，它描述了流体的运动，理解这个方程可能会很具有挑战性，在文章中，我们将利用张量语言来简化流体力学中的矢量计算，并展示如何从牛顿运动定律导出纳维尔，斯托克斯方程，向量微积分到张量分析传统的流体力学依赖于向量微积分的数学工具，它涉及点乘、叉乘和复杂的导数运算，张量分析提供了一种更简洁的方法来处理...。

中国医学科学院和北京协和医学院国家癌症中心、美国癌症协会等多个研究所曾联合进行过一项研究，该研究约涵盖了我国17%的人口，通过调查发现，2013年我国约100万的癌症死亡事件中，约有26120例与缺乏体力活动相关，反过来说，充足的锻炼是抗癌的良药，JAMA子刊上发表过一项涉及144万名受试者数据的研究称，中等到剧烈的体育活动与13种癌...。

一、JAMA子刊，运动，可降低13种癌症发生率！中国医学科学院和北京协和医学院国家癌症中心、美国癌症协会等多个研究所曾联合进行过一项研究，该研究约涵盖了我国17%的人口，通过调查发现，2013年我国约100万的癌症死亡事件中，约有26120例与缺乏体力活动相关，反过来说，充足的锻炼是抗癌的良药，JAMA子刊上发表过一项涉及144万名受...。

一、JAMA子刊，运动可降低13种癌症发生率！中国医学科学院、北京协和医学院国家癌症中心、美国癌症协会等多个研究所曾联合进行过一项大型研究，覆盖了我国约17%的人口，研究发现，2013年我国约100万的癌症死亡事件中，约26120例与缺乏体力活动相关，反过来，充足的锻炼则是抗癌的良药，JAMA子刊上发表过一项涉及144万名受试者数据的...。

导言纳维尔，斯托克斯方程是流体力学中的一个关键方程，它描述了粘性流体的运动，理解这个方程对于理解各种流体现象，如湍流和边界层，至关重要，本文将介绍如何使用张量语言来简化纳维尔，斯托克斯方程的理解，并探讨其与牛顿运动定律之间的联系，矢量微积分和张量语言传统的流体力学使用矢量微积分来对流体运动进行描述，张量语言提供了一种更简洁和通用的方法...。

导言流体力学是研究流体运动和行为的学科，纳维尔，斯托克斯方程是流体力学中最重要的方程组，它描述了流体的运动和应力，纳维尔，斯托克斯方程纳维尔，斯托克斯方程是一组偏微分方程，由法国数学家克洛德，路易·纳维和英国物理学家乔治·加布里埃尔·斯托克斯于19世纪初独立提出，它们描述了流动流体中速度、压力和应力的关系，纳维尔，斯托克斯方程式组如下...。

引言纳维尔，斯托克斯方程是流体力学中描述流体运动的基本偏微分方程组，它以其复杂性和解决它的难度而著称，通过使用张量语言，我们可以简化流体力学中的矢量计算，并更深入地理解纳维尔，斯托克斯方程，张量语言在矢量微积分中的应用张量是一种描述多维实体的数学对象，它们可以用来表示矢量、二阶张量和更复杂的对象，在矢量微积分中，张量语言可以用来简化点...。

豆腐制作，自动化时代下的轻松体验豆腐制作的传统辛酸豆腐作为一种古老的豆制品，一直深受人们喜爱，传统的手工制作方法却是一件费力辛苦的工作，古语有云，人生三苦，打铁、撑船、做豆腐，可见，做豆腐的辛劳程度可见一斑，自动化豆腐机的诞生随着科技的发展，自动化豆腐机应运而生，这一设备的出现，让豆腐制作不再是体力活，而是变得轻松省力，豆贵妃豆腐机就...。