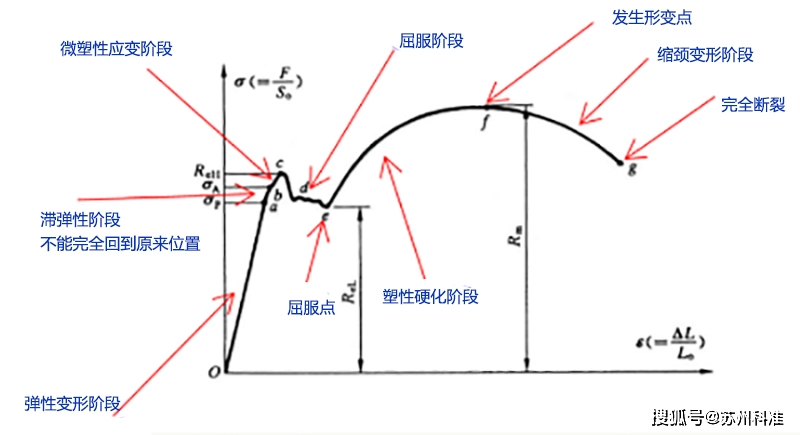
 i
n
i
dS
i
n
i
dS
球坐标系中,法向导数∂ i n i 为:
∂ i n i = (∂ê r /∂r) = (1/r)ê r
因此,第三项可以写为:
F
3
= -μ∫∫S(−pδ
ij
+ (μ + λ)Δ
ij
- μ∂
 j
u
i
)ê
j
(1/r)ê
i
dS
j
u
i
)ê
j
(1/r)ê
i
dS
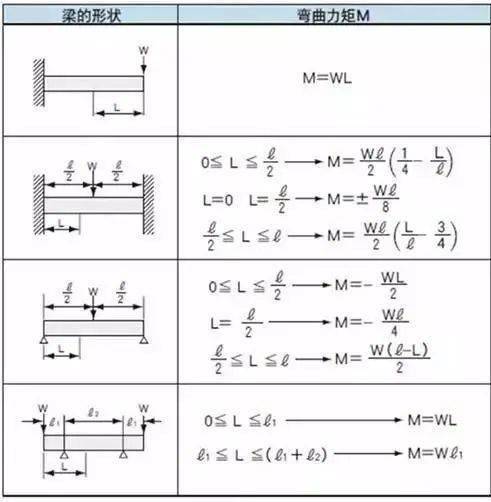
由于α=1(径向方向),因此有:
F 3 = -μ∫∫S(−pδ 11 + (μ + λ)Δ 11 - μ∂ 1 u 1 )(1/r)dS
计算出克氏符和度规分量后,得到:
F 3 = -4πμ(μ + λ)Δ 11
结论
通过微分几何的语言,我们完整地揭示了应力张量在斯托克斯定律中的作用,计算了第二项和第三项对斯托克斯力的贡献。这进一步加深了我们对固体小球在流体中运动的理解。






发表评论