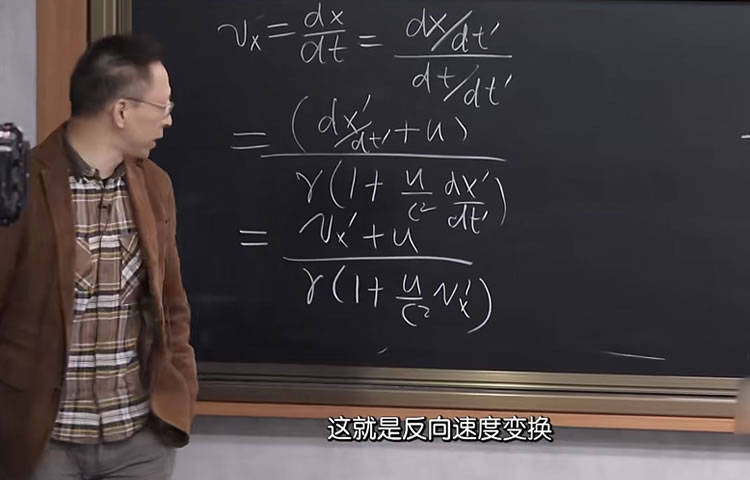
引力波:时空
涟漪的
奥秘
引言
在《
张朝阳的
物理课》第二百三十二期中,物理学博士张朝阳深入探讨了引力波的奥秘。本篇简要文章将根据张朝阳的
课程内容,介绍引力波的本质、具体形式和观测
方法。
广义相对论的基本框架
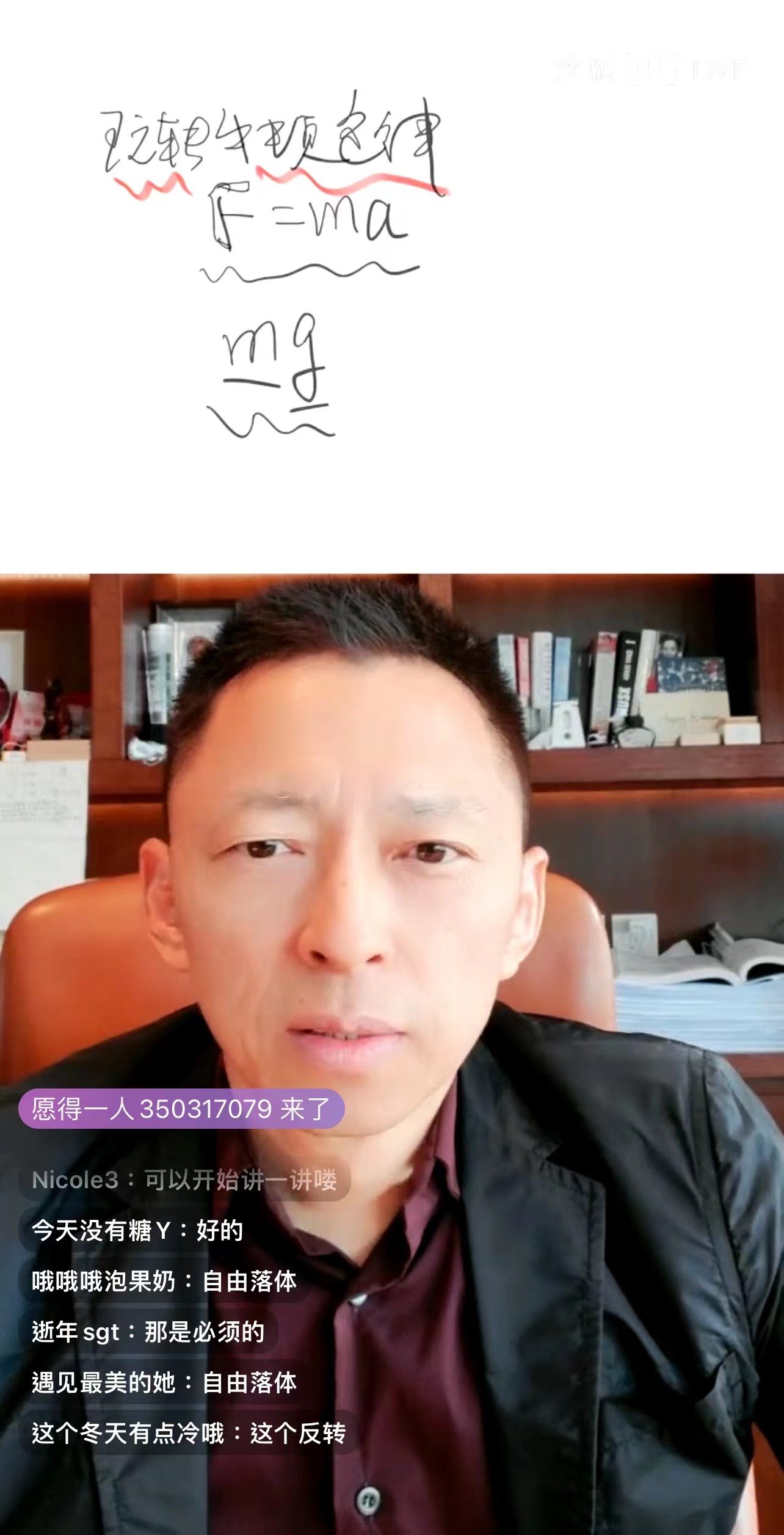
广义相对论表明,物质的存在导致时空弯曲。粒子在弯曲时空中的运动不再需要考虑引力,而是沿着一条最短路径前行。度规是一个二阶张量,描述时空的弯曲程度。
求解弱场引力波方程
度规的微扰
要求解描述引力波的方程,首先需要考虑度规的微扰。假设度规为
g_μν = η_μν + h_μν
其中,η_μν 是平直时空的度规,h_μν 是微扰。
波动方程
将微扰的度规代入广义相对论的
爱因斯坦场方程,可以得到描述 h_μν 的波动方程:
□h_μν = (1/16πG)T_μν
其中,□ 是
达朗贝尔算符,G 是万有引力常数,T_μν 是物质的应力-能量张量。
引力波的具体形式
真空引力波
在真空情况下,T_μν = 0。代入波动方程,可以得到真空引力波方程:
□h_μν = 0
此方程有平面波解:
h_μν = A_μν exp(ik_μx^μ)
其中,A_μν 是常数张量,k_μ 是波矢。
两种模式
平面波解可以分为两种模式:
加向模式 (Plus):h_μν 仅在
对角线分量上非零。
减向模式 (Minus):h_μν 仅在不同角线分量上非零。
测量可观

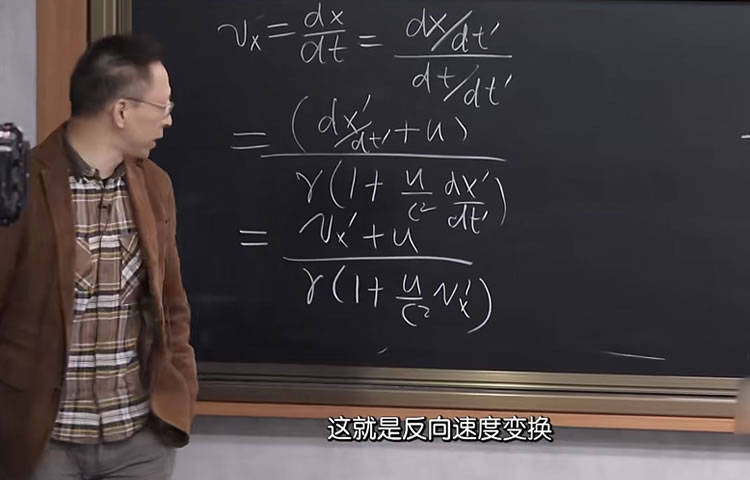 引力波:时空涟漪的奥秘
引言
在《张朝阳的物理课》第二百三十二期中,物理学博士张朝阳深入探讨了引力波的奥秘。本篇简要文章将根据张朝阳的课程内容,介绍引力波的本质、具体形式和观测方法。
广义相对论的基本框架
广义相对论表明,物质的存在导致时空弯曲。粒子在弯曲时空中的运动不再需要考虑引力,而是沿着一条最短路径前行。度规是一个二阶张量,描述时空的弯曲程度。
求解弱场引力波方程
度规的微扰
要求解描述引力波的方程,首先需要考虑度规的微扰。假设度规为
g_μν = η_μν + h_μν
其中,η_μν 是平直时空的度规,h_μν 是微扰。
波动方程
将微扰的度规代入广义相对论的爱因斯坦场方程,可以得到描述 h_μν 的波动方程:
□h_μν = (1/16πG)T_μν
其中,□ 是达朗贝尔算符,G 是万有引力常数,T_μν 是物质的应力-能量张量。
引力波的具体形式
真空引力波
在真空情况下,T_μν = 0。代入波动方程,可以得到真空引力波方程:
□h_μν = 0
此方程有平面波解:
h_μν = A_μν exp(ik_μx^μ)
其中,A_μν 是常数张量,k_μ 是波矢。
两种模式
平面波解可以分为两种模式:
加向模式 (Plus):h_μν 仅在对角线分量上非零。
减向模式 (Minus):h_μν 仅在不同角线分量上非零。
测量可观
引力波:时空涟漪的奥秘
引言
在《张朝阳的物理课》第二百三十二期中,物理学博士张朝阳深入探讨了引力波的奥秘。本篇简要文章将根据张朝阳的课程内容,介绍引力波的本质、具体形式和观测方法。
广义相对论的基本框架
广义相对论表明,物质的存在导致时空弯曲。粒子在弯曲时空中的运动不再需要考虑引力,而是沿着一条最短路径前行。度规是一个二阶张量,描述时空的弯曲程度。
求解弱场引力波方程
度规的微扰
要求解描述引力波的方程,首先需要考虑度规的微扰。假设度规为
g_μν = η_μν + h_μν
其中,η_μν 是平直时空的度规,h_μν 是微扰。
波动方程
将微扰的度规代入广义相对论的爱因斯坦场方程,可以得到描述 h_μν 的波动方程:
□h_μν = (1/16πG)T_μν
其中,□ 是达朗贝尔算符,G 是万有引力常数,T_μν 是物质的应力-能量张量。
引力波的具体形式
真空引力波
在真空情况下,T_μν = 0。代入波动方程,可以得到真空引力波方程:
□h_μν = 0
此方程有平面波解:
h_μν = A_μν exp(ik_μx^μ)
其中,A_μν 是常数张量,k_μ 是波矢。
两种模式
平面波解可以分为两种模式:
加向模式 (Plus):h_μν 仅在对角线分量上非零。
减向模式 (Minus):h_μν 仅在不同角线分量上非零。
测量可观







发表评论