导言
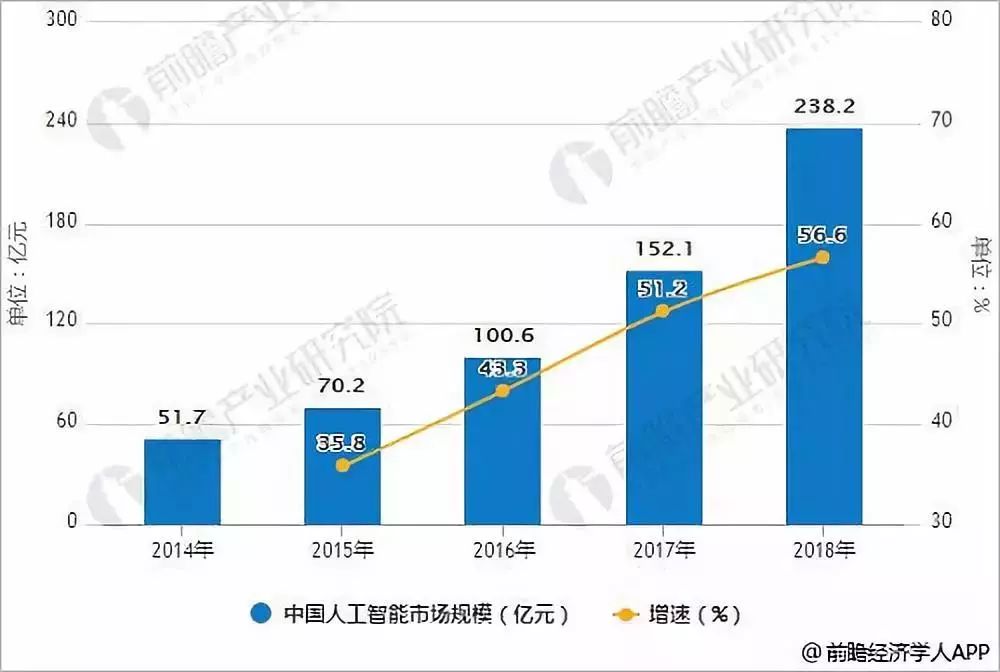
流体力学是研究流体
运动和行为的学科。纳维尔-斯托克斯方程是流体力学中最重要的方程组,它描述了流体的运动和应力。
纳维尔-斯托克斯方程
纳维尔-斯托克斯方程是一组偏微分方程,由法国数学家克洛德-路易·纳维和英国
物理学家乔治·加布里埃尔·斯托克斯于 19 世纪初独立提出。它们描述了流动流体中速度、压力和应力的关系。
纳维尔-斯托克斯方程式组如下:
```equation
\rho \frac{\partial \mathbf{v}}{\partial t} = -\nabla p + \eta \nabla^2 \mathbf{v} + \rho \mathbf{f}
```
其中:
$\rho$ 是流体的
密度
$\mathbf{v}$ 是流体的速度
$p$ 是流体的压力
$\eta$ 是流体的粘度
$\mathbf{f}$ 是作用在流体上的外力
与牛顿运动定律的关系
纳维尔-斯托克斯方程
实际上是牛顿第三定律(作用力等于反作用力)在流体中的表达。等式右侧的压强梯度项$-\nabla p$描述了流体微元的压力梯度力,粘滞项$\eta \nabla^2 \mathbf{v}$描述了流体微元的内部摩擦力。
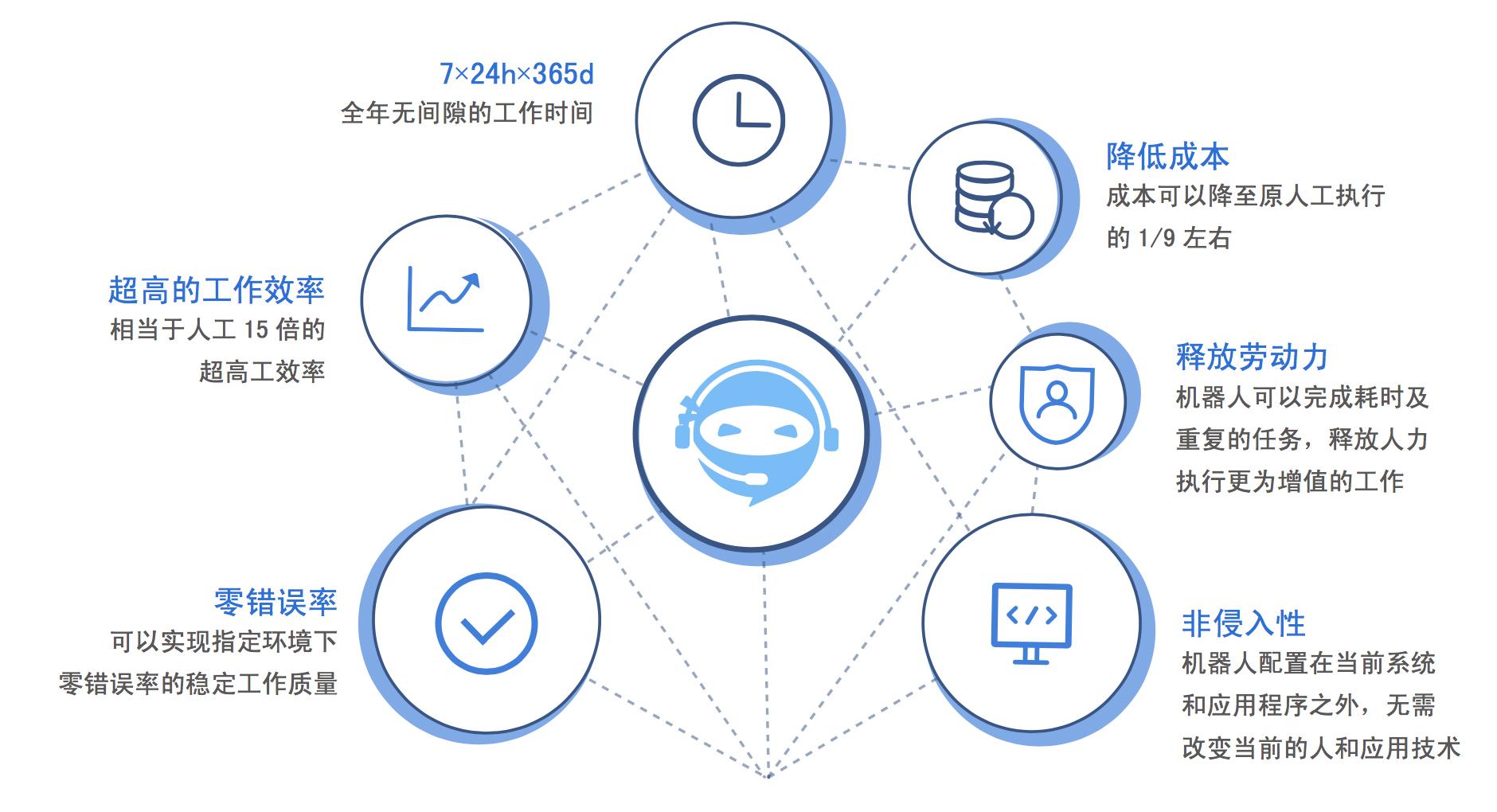
张量语言
张量语言
是一种数学语言,可以简化流体力学中的矢量计算。张量是由具有多个指标的对象组成,这些指标表示它们在不同坐标方向上的分量。
在张量语言中,矢量被视为一阶张量,二阶张量则表示应力或应变。张量语言允许使用简洁的符号表示复杂的矢量方程,并简化计算。
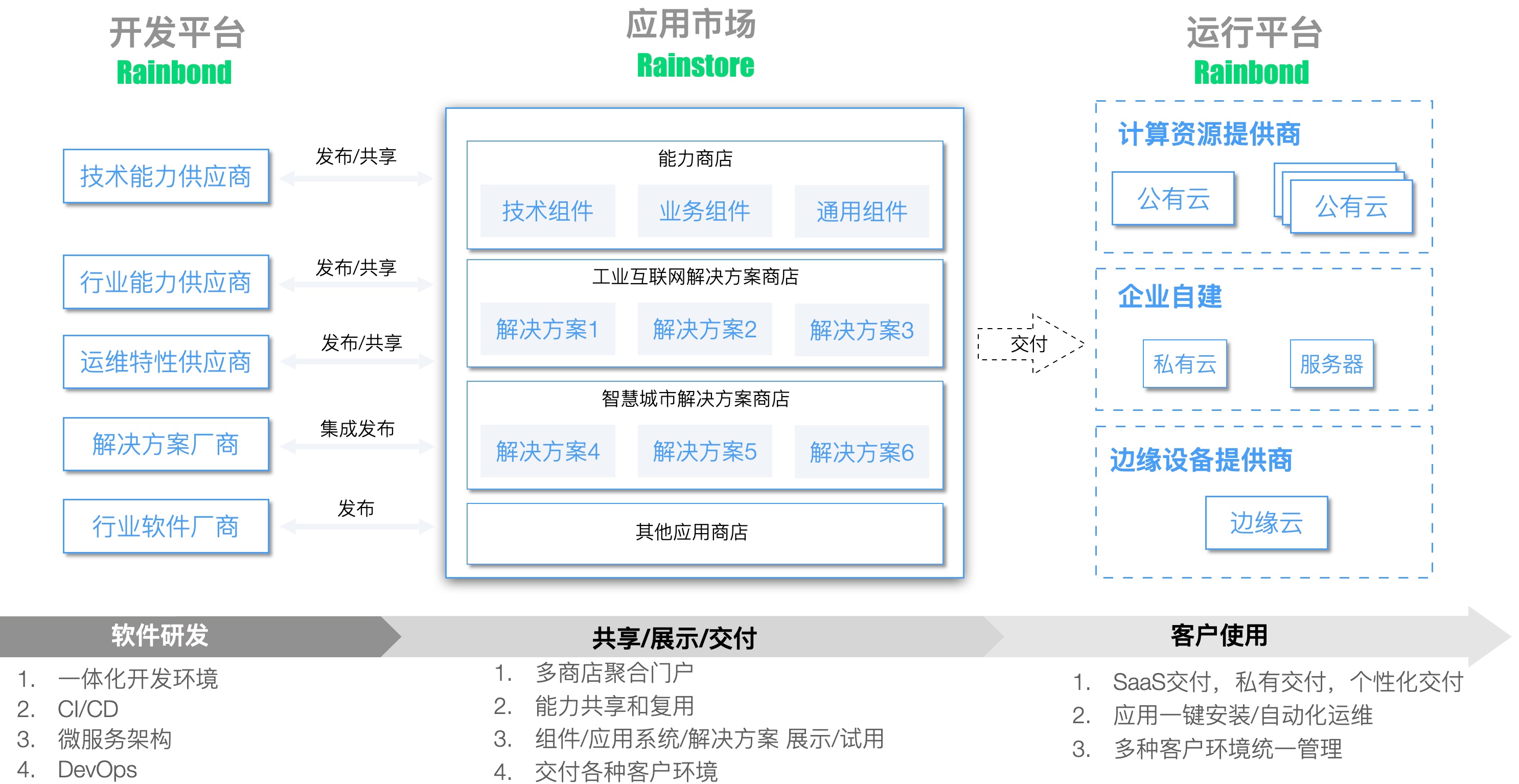
张量语言中的矢量微积分运算
使用张量语言,矢量微积分中的运算可以被极大地简化。例如:
点乘:两个一阶张量的点乘产生一个标量。
叉乘:两个一阶张量的叉乘产生一个一阶张量。
梯度:一个函数的梯度是一个一阶张量。
散度:一个一阶张量的散度是一个标量。
拉普拉斯算子:一个标量的拉普拉斯算子是一个标量。
纳维尔-斯托克斯方程的张量语言表达
纳维尔-斯托克斯方程可以用张量语言表示为:
```equation
\rho \partial_t \mathbf{v}_i = -\partial_i p + \eta \partial_j \partial_j \mathbf{v}_i + \rho f_i
```
其中:
$\partial_i$ 和 $\partial_j$ 是偏导数算子
下标 $i$ 和 $j$ 对应于空间维数
应用
张量语言在流体力学中有许多应用,
包括:
简化流体运动方程的求解
分析复杂流动的稳定性
研究湍流的性质
结论
纳维尔-斯托克斯方程是流体力学中的基石,它们描述了流体运动和应力的基本原理。张量语言提供了一种简便的方法来理解和解决这些方程组,从而加深我们对流体力学
现象的理解。









发表评论